TS EAMCET 2019 :: Mathematics :: General questions

• Mathematics - General questions

The lines represented by $5x^{2}-xy-5x+y=0$ are normals to a circle S=0 .If this circle touches  the circle  

$S'=  x^{2}+y^{2}-2x+2y-7=0$ externally , then  the equation of the chord of contact  of centre of S'=0 with respect to S=0 is 

Answer:

Explanation:

 We have,

$5x^{2}-xy-5x+y=0$  are normal to circle S=0

$\therefore$ Centre of circle S=0  is point of intersection of line

              $5x^{2}-xy-5x+y=0$

           (x-1)(5x-y)=0

x=1, 5x-y=0

$\therefore$  Centre (1,5)

Centre of circle        S'= $ x^{2}+y^{2}-2x+2y-7=0$  is (1,-1)

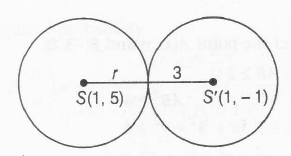
  and radius =3

 $SS'=\sqrt{(1-1)^{2}+(5+1)^{2}}=6$

 $\therefore$       r= SS'-3=6-3=3

Equation of circle 

 S= $ (x-1)^{2}+(y-5)^{2}= (3)^{2}$

 = $x^{2}+y^{2}-2x-10y+17=0$

 Equation of chord of contact at (1,-1) to S=0 is

 $x-y-2\frac{(x-1)}{2}-10\frac{(y-1)}{2}+17=0$

 x-y-x-1-5y+5+17=0

 $\Rightarrow$     -6y+21=0

$\Rightarrow$       2y-7=0

In a communication network , ninety eight precent of messages are transmitted with no error.If a random variable  X denotes the number of incorrectly transmitted messages , then the probability that atmost one message is transmitted incorrectly out of 500 messages sent, is

Answer:

Explanation:

Here,

 n=500 ,p=2%, q=98%

Required probability

 $P(X\leq1)=P(X=0)+P(X=1)$

 $=\frac{\lambda^{0}e^{-\lambda}}{0!}+\frac{\lambda^{}e^{-\lambda}}{1!}$

  $P(X\leq1)=e^{-\lambda}(1+\lambda)$

 = $e^{-10}(1+10)$                   [$\because  \lambda=np= 500 \times \frac{2}{100}=10$]

= $\frac{11}{e^{10}}$

Bag I contains 3 red and 4 black  balls , Bag II contains 5 red and 6 black balls .If one ball is drawn at random from one of the bags and it is found to be red , then the probability  that it was drawn from Bag II, is 

Answer:

Explanation:

Bag 1 contains 3 red and 4 black balls bag II  contains 5 red and 6 black balls

 P(I)=$\frac{1}{2}$,P(II)=$\frac{1}{2}$

$P\left(\frac{R}{I}\right)=\frac{3}{7}, P\left(\frac{R}{II}\right)=\frac{5}{11}$

$\therefore$ Required probability

$P\left(\frac{II}{R}\right)=\frac{P(II) \times P\left(\frac{R}{II}\right)}{P(I)\times P(R/I)+P(II)+P\left(\frac{R}{II}\right)}$

$=\frac{\frac{1}{2}\times \frac{5}{11}}{\frac{1}{2}\times\frac{3}{7}+\frac{1}{2}\times\frac{5}{11}}=\frac{35}{68}$

If OA= $\hat{i}+2\hat{j}+3\hat{k}$ and OB= $4 \hat{i}+\hat{k}$ are the position vectors of the points  A and B , then the position vector of a point  on the line passing through  B and parallel to the vector   OA x OB which is at a distance of $\sqrt{189}$  units from B is

Answer:

Explanation:

We have,

 OA=$\hat{i}+2\hat{j}+3\hat{k}$ and OB= $4 \hat{i}+\hat{k}$

 $\because$   $OA \times OB=\begin{bmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & 2&3 \\4 &0&1 \end{bmatrix}= 2 \hat{i}+11\hat{j}-8\hat{k}$

 equation of line passing through B and parallel to  OA x OB is

 r= $4\hat{i}+\hat{k}+\lambda  (2 \hat{i}+11 \hat{j}-8\hat{k})$

     r= $(4+2 \lambda)\hat{i}+11 \lambda \hat{j}+(1-8 \lambda) \hat{k}$

Distance from B to line  is $\sqrt {189}$

 $\therefore$    $\sqrt{189}$=  $\sqrt{(4+2\lambda-4)^{2}+(11\lambda)^{2}+(1-8 \lambda -1)^{2}}$

 189= $4\lambda^{2}+121\lambda^{2}+64 \lambda^{2}$

  189= 189 $\lambda ^{2}$

$\lambda$= $\pm$ 1

$\therefore$ Position vector ;ie on line  B

r= $6 \hat{i}+11\hat{j}-7 \hat{k}$

 p₁,p₂,p₃  arte the altitudes  of a triangle ABC drawn from the vertices A,B and C respecively . If $\triangle$  is the area  of the triangle and 2s is the sum of its sides a,b and c , then $\frac{1}{p_{1}}+\frac{1}{p_{2}}-\frac{1}{p_{3}}$=

Answer:

Explanation:

Given

 BC=a,  AC-b

AB=c, AD=P₁

BE= p₂ , CF= p₃

 In $\triangle ABC $

       $\sin B=\frac {p_{1}}{c} \Rightarrow  \frac{1}{p_{1}}= \frac {1}{c \sin B}$

 Similarly  ,    $\frac{1}{p_{2}}=\frac{1}{a \sin C}$

and      $\frac{1}{p_{1}}=\frac{1}{b \sin A}$

$\therefore$     $\frac{1}{p_{1}}+\frac{1}{p_{2}}-\frac{1}{p_{3}}=\frac{1}{c\sin B}+\frac{1}{a\sin C}-\frac{1}{b\sin A}$

 =$\frac{a}{2 \triangle}+\frac{b}{2 \triangle}-\frac{c}{2 \triangle}=\frac{1}{2 \triangle}(a+b-c)=\frac {2(s-c)}{2 \triangle}=\frac{(s-c)}{\triangle}$

$\therefore$  $\frac{1}{p_{1}}+\frac{1}{p_{2}}-\frac{1}{p_{3}}$=  $\frac{s }{\triangle}$

• Mathematics - General questions